Надежность - свойство объекта (изделия, конструкции, здания или сооружения) сохранять значения установленных параметров функционирования в определенных пределах, соответствующих заданным режимам и условиям эксплуатации. Это - комплексное свойство, которое может включить ремонтопригодность, безотказность и долговечность.
Мерой надежности является безотказность работы за заданный срок службы.
Ремонтопригодность - способность системы к предупреждению, обнаружению и устранению различных отказов и отклонений путем проведения ремонтов.
Безотказность - свойство объекта непрерывно сохранять работоспособность в течение некоторого времени.
Долговечность - свойство объекта сохранять работоспособность до наступления предельного состояния с необходимыми перерывами на ремонт. Для зданий и сооружений - предельный срок службы, в течение которого они сохраняют требуемые эксплуатационные качества.
Различают долговечность моральную и физическую. Моральная долговечность характеризуется сроком службы здания или сооружения до того момента, когда они перестают отвечать изменяющимся условиям эксплуатации или режима технологических процессов. Физическая долговечность определяется продолжительностью износа основных несущих конструкций и элементов под действием нагрузок и физико-химических факторов.
Отказ - это утеря работоспособности, наступающая внезапно или постоянно; это - реализация состояний объекта, при которых он не сможет выполнять свои функции в течение установленного срока службы [100]; скачкообразный переход системы из работоспособного состояния в неработоспособное называют внезапным отказом. Отказы можно классифицировать в зависимости от: причин возникновения, последствий, срока эксплуатации, скорости проявления.
Физический износ - ухудшение технического состояния, потеря эксплуатационных, прочностных и других качеств.
Предельное состояние - состояние, при переходе за которое сооружение перестает соответствовать поставленным требованиям [143]. Различают две группы предельных состояний.
К первой относят состояния, при выходе за которые возникает полная потеря пригодности к эксплуатации, - это общая потеря устойчивости;
163
потеря устойчивости положения; разрушение любого характера; переход в изменяемую систему; качественное изменение конфигурации; состояния, при которых прекращается эксплуатация вследствие: чрезмерных деформаций ползучести и пластичности, сдвигов в соединениях или чрезмерного раскрытия трещин, опасности для здоровья и жизни людей, возможного материального ущерба.
Ко второй группе относятся предельные состояния, при выходе за которые затрудняется нормальная эксплуатация вследствие: недопустимых перемещений и уровней колебании; недопустимых изменений положения и раскрытия трещин. При выходе за это состояние не возникает опасности для жизни и здоровья людей, материальный ущерб ограничен.
Сооружение может отказать по многим предельным состояниям.
Количественно предельные состояния задают пределами для деформаций, напряжений, перемещений и разности перемещений, поворотов, раскрытия трещин, амплитуд колебаний и других параметров.
Основы теории изложены в [143]. Полагают, что конструкции могут быть в двух состояниях: V - отказ и V - безотказная работа. Вероятность отказа Pf = P(V) есть вероятность того, что в течение рассматриваемого времени будет превзойдено предельное состояние. Вероятность безотказной работы Ps = P(V) есть вероятность того, что за время Т не будет выхода за предельное состояние. Имеет место равенство Pf + Ps = 1. С возрастанием периода времени увеличивается вероятность отказа, т.е. Pf является монотонно возрастающей функцией времени. Дополнение является функцией надежности:
L(t) = l-Pf (t) = Ps (t).(6.1)
Она представляет собой вероятность того, что сооружение просуществует время t. L(t) является монотонно убывающей функцией времени.
Основой требований по надежности является опыт предыдущего строительства [143].
Плотность отказов ht (t) (размерность Т-1) является характеристикой надежности во времени. Она определяется как вероятность того, что безотказно работающее до момента t сооружение откажет в последующий интервал времени (t,t + Δt) [143]. Плотность отказов, как правило, имеет вид, представленный на рис. 6. 1
В начале срока существования (фаза 1) часто встречаются выбросы, вызванные низким качеством работ и материалов. Во второй фазе плотность отказов относительно постоянна и вызывается перегрузками. В третьей фазе существования сооружения плотность отказов вновь возрастает за счет падения сопротивления из-за процессов усталости, старения или коррозии.
164
В теории надежности предельные состояния могут быть выражены базисными переменными X; [143]. Совокупность их представляют случайным вектором
X = ( X1...X2)
(6.2)
При g(x1,x2,...,xn)<0 наступает отказ по предельному состоянию, a g(x) = g(x1,х2,...,хn)>0 соответствует безотказной работе.
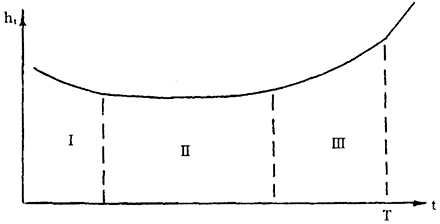Рис. 6.1. Характерный график плотности отказов
Уравнение предельного состояния записывают в виде
g(x) = g(x1,x2 ,...,xn) = 0
(6.3)
Уравнение 6.3 в пространстве базисных переменных представляет собой гиперповерхность, которая делит все пространство на две части: область отказа и безопасную область. Само предельное состояние часто относят к безопасной области. В таком случае геометрически предельное состояние представляетвнешнюю поверхность безопасной области (рис. 6.2).
Рис. 6.2. К определению предельного состояния
в пространстве базисных переменных:I - область отказа; II - область безотказной работы
165
Обозначая через r = gR (xR1 ,xR2 ,...) базисные переменные, определяющие несущую способность, а через s = gs1 (xs2,хs,...) – определяющее внешнее воздействие, можно записать уравнение предельного равновесия в виде
g(x) = r-s = 0.
(6.4)
В статистических системах отказ может произойти по нескольким состояниям. Конструкции, состоящие из нескольких элементов, могут иметь многие механизмы отказа. Тогда имеем систему из п уравнений предельных состоянии
{
g1(x1,x2,...,xm) = 0;
g2(x1,x2,...,xm) = 0,
...
gn(x1,x2,...,xm) = 0.
(6.5)
Различают системы с последовательным и с параллельным соединением элементов. В первых система отказывает, если превзойдено какое-либо из п предельных состояний, т.е. g1(х) < 0 или g2(х) < 0... или gn (х) < 0. Во вторых система отказывает, если превзойдены все п предельных состояний, т.е. g1(x)<0 и g2(х)<0... и gn(x)<0.
Комбинация параллельных и последовательных систем дает смешанную систему.
Важна не только частота появления отказов, но и тяжесть их последствий для общества. Поэтому вводится в рассмотрение понятие риска rf как произведение вероятности отказа Pf и ожидаемых последствий отказа Vf, т.е.
rf=Pf·Vf.
(6.6)
Выделяют [143] три группы последствий отказа: для жизни и здоровья людей, экономические, для окружающей среды и культурных ценностей. Наступление отказа резко ведет только к одной группе последствий.
Коэффициент запаса. Мерой безопасности при проектировании является коэффициент запаса у, определяемый как отношение сопротивления к нагрузке. Уравнение предельного состояния в этом случае имеет вид:
g (x(n),γ) = r(n) - γS(n) = 0
(6.7)
или
γ = r
(n) / S
(n), r
(n) =
gR(x
(n)R1, x
(n)R2,...);
где S(n) = gS(x(n)S1, x(n)S2), x(n)R1 - нормативные величины базисных переменных, определяющих несущую способность; x(n)S1- нормативные величины, определяющие внешнее воздействие.
166
Расчетныезначения базисных переменных xi, xRi, x Sj обозначаются
xi(r), xRi(r), x, xRi(r), xi(r), xSi(r)
Различают пять типов частных коэффициентов надежности:
- по назначению γn - учитывает экономическое и социальное значения, размеры последствий отказов и сроки службы различных сооружений;
- по нагрузке γf - учитывает изменчивость нагрузок и возможные отклонения от нормальных условий эксплуатации;
- по материалу γm - учитывает неизбежную изменчивость и разброс свойств строительных материалов и грунтов;
- коэффициент сочетаний нагрузокψ - учитывает малую вероятность
- одновременного появления наибольших значений различных нагрузок; рассматривается только вместе с правилом сочетания нагрузок;
- коэффициент условий работы γd - учитывает неточности расчетной модели, возникающие за счет ее упрощения и идеализации.
По отношению к нагрузкам коэффициенты вводятся в виде множителей, а к материалу - в виде делителей. В некоторых нормативах коэффициент условий работы для материала в уравнении предельного состояния также выступает как множитель.
Коэффициент надежности по назначению имеет форму общего коэффициента запаса, на который умножаются все нагрузки. Для сооружений среднего класса γn = 1, имеющих большое значение γn > 1, для прочих γn < 1. В ЦНИИСКе γn предложено представлять в виде произведения двух коэффициентов
γn = γn1 · γn2
где γn1, - коэффициент, учитывающий возможный ущерб дли жизни и здоровья людей; γn2 - коэффициент, учитывающий возможный материальный ущерб; γn1 -0,9; 1,0 и 1,1; γn2 = 0,9; 0,95 и 1.
Коэффициент γn1= 1,1 принимают для сооружений, где постоянно или периодически находится большое число людей (театры, клубы, вокзалы, детские сады, АЭС, мосты и т.д.); уп! = 1 - для сооружений, где постоянно или периодически может находиться среднее число людей (жилые дома, общественные и промышленные здания, не входящие в первую группу); γn1 - 0,9 - для сооружений, где люди бывают редко (теплицы, склады, мачты ЛЭП, антенны и т.д.).
Коэффициент γn2 = 1 принимают для сооружений, имеющих первостепенное значение для всего народного хозяйства (главные цеха фабрик и заводов, главные здания электростанций, домны, элеваторы и т.д.); γn2 = 0,95 - для сооружений, имеющих первостепенное значение для отдельных
167
отраслей народного хозяйства (вспомогательные промышленные здания, склады, дымовые трубы, вокзалы, мосты и т.д.), γn2 - 0,9 - для сооружений, не играющих решающей роли в народном хозяйстве (теплицы, телефонные линии, склады и т.д.).
Коэффициент надежности по нагрузке зависит от рассматриваемого предельного состояния и принимается большим единицы, если данное воздействие ведет к повышению нагрузки, и меньше единицы, если оно уменьшает нагрузку.
Сочетания нагрузок. Правило сочетания представляет собой предписание, согласно которому по расчетным значениям многих кратковременных нагрузок можно найти расчетное значение комбинаций. Оно должно удовлетворять условию, чтобы запроектированная конструкция имела примерно равную надежность для всех возможных сочетаний нагрузок.
В [143] предлагается установить единый коэффициент ψт для всех m, участвующих в сочетании нагрузок. Так как конструкция должна быть проверена и на каждую нагрузку, правило сочетаний представляется в виде:
| gs = max |
{ |
gs(xs1(r))
gs(xs2(r))
...
gs(xsm(r))
gs(ψmxs1(r), ψmxs2(r) ... ψmxsm(r)).
|
(6.5)
Для частного случая упругой работы конструкции (при линейной зависимости между нагрузками и напряжениями) это правило может быть записано в виде
| gs = max |
{ |
c1xs1(r)
c2xs2(r)
...
cmxsm(r)
Ψm nΣi = 1 ci xci(r) |
(6.6)
При m изменяющихся во времени нагрузках возникает m сочетаний. Определяющим является наибольшее значение из всех комбинаций.
Принцип равнопрочности. Конструкцию считают равнопрочной, если она удовлетворяет следующим требованиям [144]:
- не содержит опасных трещиноподобных дефектов металлургического или технологического происхождения;
- работает в условиях, исключающих опасное развитие в ней эксплуатационных трещин за требуемый промежуток времени;
- локальное разрушение приводит к разрушению или потере работоспособности конструкции в целом.
168
Первые два допущения позволяют считать конструкцию бездефектной и для определения условия локального разрушения пользоваться феноменологическими теориями, в которых принимается функциональная зависимость между критическими значениями напряжений σij, деформаций εij, температуры Т, времени t, т.е.
f (σij, εij, T, t) = 0, (i, j = 1,2,3).
(6.7)
При f <0 локального разрушения не происходит, f = 0 - происходит разрушение, а состояние f > 0 - невозможно.
Основными теориями прочности являются теории Галилея, Понселе, Кулона, Мора, Треска, Губера, Мизеса, Генки и др.
Согласно экспериментальным данным при одноосном растяжении постоянной нагрузкой для металлов и полимеров
| σ1 = |
u |
− |
RT |
ln |
t |
(t > τ0), |
γ |
γ |
τ0 |
(6.8)
где σ1 - временное сопротивление; u - энергия активации; γ - структурная постоянная; R - газовая постоянная; τ0 - время пробега упругой волны на межатомное расстояние (τ0≈10-12 с); Т - абсолютная температура; t - длительность действия нагрузки.
Существенным недостатком теорий прочности является то, что в случае сложного напряженного состояния локальное разрушение часто не приводит к разрушению всей конструкции.
Условие равнопрочности является условием минимальной массы конструкции.
Критерий наибольших нормальных напряжений (Гипотеза Г.Галилея). Пластическая деформация или разрушение хрупкого материала наступает тогда, когда наибольшее по абсолютной величине главное напряжение достигает некоторого предельного значения. Соответствующее условие прочности имеет вид
|σj| ≤ σ0(j = l,2,3),
(6.9)
где σ0 - предельное значение напряжения.
Предельная поверхность - куб со стороной σ0. Эта теория мало применима при действии сжимающих напряжений.
Критерий наибольших линейных деформаций. Разрушение материала начинается тогда, когда наибольшая по абсолютной величине линейная
169
деформация удлинения достигает предельного значения. Этому критерию соответствуют условия прочности
| { |
σ1 - (σ2 + σ3) = σ0 |
| σ2 - (σ3 + σ1) = σ0 |
| σ3 - (σ1 + σ2) = σ0 |
(6.10)
Область применения этой теории ограничивается хрупкими материалами. Первая и вторая теории прочности не применимы, когда разрушение пластичное.
Критерий наибольших касательных напряжений (Теория Треска). Пластические деформации наступают тогда, когда наибольшее касательное напряжение достигает предельного значения. Условие прочности принимается в виде:
| { |
σ1 - σ2 = ±σ0 |
| σ2 - σ3 = ±σ0 |
| σ3 - σ1 = ±σ0 |
(6.11)
Предельная поверхность представляет собой правильную шестигранную призматическую поверхность с осью, направленной по пространственной диагонали. Критерий по наибольшим касательным напряжениям применим к пластическим материалам и к определению момента перехода материала в состояние пластического деформирования.
Энергетический критерий прочности. Материал переходит в состояние пластического деформирования тогда, когда полная удельная энергия деформации достигает некоторого предельного значения. Условие прочности имеет вид:
σ12 + σ22 + σ32-2v(σ1σ2 + σ2σ3 + σ3σ1) ≤ σ02
Уравнение предельной поверхности
σ12 + σ22 + σ32-2v(σ1σ2 + σ2σ3 + σ3σ1) - σ02=0
Этот критерий справедлив для пластических материалов.
Критерий прочности Губера-Мизеса-Генки. Пластическое состояние (разрушение) наступает тогда, когда удельная энергия формоизменения достигает предельного значения.
Этому критерию соответствует условие прочности
(σ1 - σ2)2 + (σ2- σ3)2 + (σ3 - σ1)2≤ σ02
170
Уравнение предельной поверхности имеет вид
σ12 + σ22 + σ32 - σ1σ2 - σ2σ3 - σ3σ1 - σ02=0
171
