В закладки | Стартовая  
 
Навигация по сайту
Реклама
Реклама
Реклама
Библиотека
151 :: 152 :: Содержание

ПРИЛОЖЕНИЕ 18.5

Расчет водопроводной кольцевой сети с применением ЭВМ

Исходные данные.

В качестве примера возьмем сеть, изображенную на рис. 18.5.1. Подача в первый узел Q*1 = 370 л/с, подача в шестой узел Q*6 = 30 л/с, отборы в узлах: Q1 - 50 л/с, Q2 = 25 л/с, Q3 = 100 л/с, Q4 = 150 л/с, Q5 - 75 л/с. Геодезические отметки узлов: №1 - 150,50м, №2 -153,20м, №3 - 155,10м, №4 -149,00м, №5 - 151,60м, №6 -156,30м.

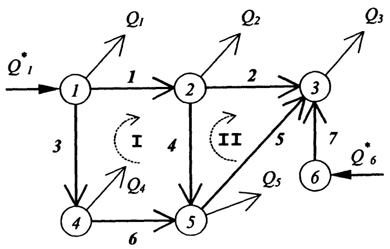
Рис. 18.5.1. Расчетная схема кольцевой сети.
Рис. 18.5.1. Расчетная схема кольцевой сети.

Длины участков: (1-2) - 550 м, (2-3) - 430 м, (1-4) - 210 м, (2-5) - 220 м, (3-5) - 570 м, (4-5) -510м, (3-6) - 300 м. Трубы на всех участках - стальные электросварные новые. Диаметр труб на участках (1-2), (1-4) и (3-5) - 350 мм, на участках (2-3), (4-5) и (3-6) - 300 мм, на участке (2-5) - 250 мм.

Минимальный диаметр - 100 мм; необходимый напор в узлах - 22 м; коэффициент суточной и часовой неравномерности водопотребления - соответственно 1,2 и 1,44; стоимость электроэнергии - 0,02 руб./кВт·ч; срок окупаемости - 7 лет. Оптимизации диаметров не требуется.

Исходные данные в этом случае будут выглядеть так:

  • CountAreas = 7; CountNodes = 6; CountRings = 2; MaxCountAreas = 4;
  • Rashod = -320; 25; 100; 150; 75; -30;
  • Z = 150,5; 153,2; 155;1; 149,0; 151,6; 156,3;
  • L = 550; 430; 210; 220; 570; 510; 300;
  • Mater = 3; 3; 3; 3; 3; 3; 3;
  • NomerD= 12; 11; 12; 10; 12; 11; 11;
  • MinH = 22; MinDiam = 100;
  • TypeOptim = 0; Kday = 1,2; Khour = 1,44;
  • Sigma = 0,02; Srok = 7.
Nodes = 1, 2, Rings = 1, 4, -6, -3,
2, 3, 2, -5, -4, 0;
1,4,  
2,5,  
5,3,  
4,5,  
6,3;  

По уравнениям (14.67-14.72) и исходным данным формируется двухмерный массив-матрица А. Структура этой матрицы представлена на рис. 18.5.2.

После прямого хода метода Гаусса матрица А будет иметь следующий вид:

Рис. 18.5.2. Структура матрицы А
Рис. 18.5.2. Структура матрицы А

151

1 0 1 0 0 0 0 320
0 1 1 1 0 0 0 295
0 0 1 1 -1 0 -1 195
0 0 0 1 -1 1 -1 45
0 0 0 0 1 -4 1 -65
0 0 0 0 0 1 -0,091 22,727
0 0 0 0 0 0 1 30

И после обратного хода получаем результат - вектор расходов на участках Q= 144,55; 63,18; 175,46; 56,36; 6,82; 25,46; 30,0.

Затем производится увязка сети по методу Лобачева-Кросса, ход которой приведен в табл. 18.5.1.

Таблица 18.5.1

Увязка кольцевой сети1

Итерация Расход на участках, л/с Кольцо №1 Кольцо №2
1 2 3 4 5 6 7 ∑Δh, м Δq, л/с ∑Δh, м Δq, л/с
- 144,55 63,18 175,46 5636 6,82 25,46 30,0 3,05 -18,12 -0,01 0,14
1 126,42 6333 193,58 38,10 6,68 43,58 -"- 0,16 -1,00 0,78 -8,51
2 125,42 54,82 194,58 45,61 15,18 44,58 -"- 0,33 -1,96 0,08 -0,78
3 123,46 54,04 196,54 44,43 15,96 46,54 -"- 0,06 -034 0,09 -0,89
4 123,12 53,15 196,88 44,98 16,85 46,88 -"- 0,04 -0,23 0,02 -0,22
5 122,89 52,93 197,11 44,96 17,07 47,11 -"- - - - -

Примечание: * ΣΔh - сумма потерь напора по кольцу, Δq - поправочный раход

Полученные результаты расчета водопроводной сети с применением ЭВМ сведены в табл. 18.5.2. В этой таблице так же для сравнения показаны результаты расчета с использованием всех трех типов оптимизации диаметров (п. 14.5).

Таблица 18.5.2

Результаты расчета водопроводной сети с оптимизацией

Показатель Тип оптимизации Участки
1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9
Направление 0 1-2 2-3 1-4 2-5 5-3 4-5 6-3
1 -"- -"- -"- -"- -"- -"- -"-
2 -"- -"- -"- -"- -"- -"- -"-
3 -"- -"- -"- -"- -"- -"- -"-
Расход, л/с 0 122,89 52,93 197,11 44,96 17,07 47,11 30,0
1 99,88 66,56 220,012 8,32 3,44 70,12 -"-
2 149,13 69,60 170,87 54,52 0,40 20,87 -"-
3 99,88 66,56 220,012 8,32 3,44 70,12 -"-
Скорость, м/с 0 1,19 0,70 1,90 0,84 0,16 0,62 0,40
1 1,32 1,24 1,65 0,80 0,33 70,12 1,30
2 1,44 1,30 1,65 1,58 0,04 1,05 -"-
3 1,32 1,24 1,65 0,80 0,33 70,12 -"-
Потери напора, м 0 3,12 1,12 3,04 1,00 0,089 1,05 0,28
1 4,65 4,08 1,94 2,69 1,40 5,37 5,44
2 4,56 4,46 2,29 4,44 0,04 6,73 -"-
3 4,65 4,08 1,94 2,69 1,40 5,37 -"-
Диаметр, мм 0 350 300 350 250 350 300 300
1 300 250 400 100 100 250 175
2 350 250 350 200 100 150 -"-
3 300 250 400 100 100 250 -"-

151

Продолжение табл. 18.5.2

1 2 3 4 5 6 7 8 9
    Узлы
1 2 3 4 5 6
Свободный напор, м 0 31,76 25,94 22,92 30,22 26,53 22,00
1 35,23 27,98 22,00 34,89 26,90 26,24
2 35,62 28,36 22,00 34,83 25,52 -"-
3 35,23 27,98 22,00 34,89 26,90 -"-
Экономический фактор 0,31

Как видно из таблицы, результаты расчета одинаковы при оптимизации диаметров, начиная с текущих и максимальных. Направления потоков не изменялись.

152

1 ∑Δh - сумма потерь напора по кольцу, Δq - поправочный расход.
151 :: 152 :: Содержание
Lib4all.Ru © 2010.
Корпоративная почта для бизнеса Tendence.ru