Постановка задачи
Для алгоритмов расчета водопроводной сети с использованием вычислительной техники принимаются следующие условия и ограничения:
- - сеть должна быть плоской;
- - сеть может содержать не только кольца, но и тупики; давление в сети не оказывает влияние на узловые отборы воды;
47
- - в сети может быть несколько точек подачи воды;
- - расчетные данные об участках должны содержать сведения о длине, выбранных материалах и диаметрах труб;
- - расчетные данные об узлах должны содержать сведения о геодезических отметках и узловых расходах;
- - для оптимизации диаметров должны быть введены дополнительные и технико-экономические данные (например, коэффициенты часовой и суточной неравномерности водопотребления, стоимость электроэнергии, срок окупаемости и т.д).
В ходе расчета сети должны быть определены:
- - расходы, потери напора, скорости на участках и оптимизированные (экономически наивыгоднейшие) диаметры,
- - величины свободного напора в узлах сети с учетом заданного необходимого напора.
Общий ход расчета сети заключается в следующем: сперва производится начальное распределение расходов на участках в соответствии с первым законом Кирхгофа, затем происходит увязка сети - расчет участковых расходов при соблюдении второго закона Кирхгофа, следующий этап - оптимизация диаметров в соответствии с предельными экономическими расходами, и, наконец, расчет свободных напоров в узлах сети.
Реализация алгоритмов расчета может быть выполнена в виде программы WaterRings. Описание подпрограмм, входящих в основную программу, приведено в табл. 14.27.
Таблица 14.27
Основные подпрограммы, используемые в программе
| Название |
Описание |
| FillingA |
Формирование матрицы линейных уравнений для начального потокораспределения |
| BeginStreamAllocation |
Решение задачи начального потокораспределения |
| Uvjazka |
Увязка расходов на участках по методу Лобачева-Кросса |
| Optimize |
Оптимизация диаметров труб на участках |
| CalcH |
Расчет свободных напоров в узлах |
Переменные и константы
В табл. 14.28 и 14.29 описаны переменные и константы, доступные всем алгоритмам расчета водопроводной сети. Материалы труб и сортамент диаметров взят из /14/. В табл. 14.30 приведены коды труб, используемые в программе, и формулы для расчета удельного гидравлического сопротивления для 13-ти различных видов труб /14/. Табл. 14.31 содержит коэффициенты и показатели степени, взятые в расчетах предельных расходов /15/ (alfa и п - показатели степени, характеризующие режим работы труб; К и р - коэффициент и показатель степени в формуле, определяющей потери напора на единицу длины трубопровода; R - сумма амортизационных отчислений, включая затраты на капитальный ремонт и отчислений на текущий ремонт; b - коэффициент, зависящий от условий строительства). Расчетные диаметры /14/, которые были использованы в компьютерной программе, приведены в табл. 14.32.
Таблица 14.28
Переменные, используемые в алгоритмах и программе
| Переменная |
Описание |
| 1 |
2 |
| Простые переменные |
|
| CountAreas |
количество участков в сети |
| CountRings |
количество колец в сети |
| CountNodes |
количество узлов в сети |
| MaxCountAreas |
максимальное количество участков в одном кольце |
48
Продолжение табл. 14.28
| 1 |
2 |
| MinH |
необходимый напор в узлах, м |
| MinDiam |
минимальный диаметр при оптимизации, мм |
| TypeOptim |
шифр вида оптимизации |
| Kday |
коэффициент суточной неравномерности водопотребления |
| Khour |
коэффициент часовой неравномерности водопотребления |
| Sigma |
стоимость электроэнергии, руб./(кВт·ч) |
| Srok |
срок окупаемости, годы |
| Массивы |
|
| Nodes |
двухмерный массив узлов сети, состоящий из CountAreas строк (каждая строка описывает один участок) и двух столбцов: первый столбец содержит номера подающих узлов, второй - номера принимающих узлов в участках |
| Rings |
двухмерный массив колец сети, состоящий из CountRings строк (по количеству колец) и MaxCountAreas столбцов (по максимальному количеству участков в кольце). Каждый элемент этого массива содержит номер участка |
| SigmaDH |
одномерный массив, содержащий CountRings значений сумм потерь напора по каждому кольцу (т.е. невязку), м |
| A |
двухмерный массив, реализующий в матричной форме систему линейных уравнений для решения задачи начального потокораспределения |
| Одномерные массивы, содержащие данные об узлах (длина каждого массива - CountNodes) |
|
| Rashod |
расход в узле (узловой расход), л/с |
| Z |
геодезическая отметка узла, м |
| H |
свободный напор в узле, м |
| Одномерные массивы, содержащие данные об участках (длина каждого массива - CountAreas) |
|
| Q |
расход на участке (участковые расходы), л/с |
| L |
длина участка, м |
| V |
скорость воды на участке, м/с |
| S |
удельное сопротивление труб на участке, с2/м6 |
| Mater |
код материала труб на участке |
| NomerD |
код диаметра труб на участке |
| DH |
потери напора на участке, м |
| Efactor |
экономический фактор для трубопровода на участке |
Таблица 14.29
Константы, используемые в алгоритмах и программе
| Константа |
Описание |
| Epsilon |
допустимая невязка в кольцах (0,05 м) |
| Eta |
КПД насосных агрегатов, подающих воду (0,7) |
| К0 |
коэффициент, учитывающий возможный рост водопотребления по годам (1,02) |
| KoeffOptimDiam |
одномерный массив, содержащий 5 элементов - записей с коэффициентами n,K,p,alfa,R и b для расчета предельных расходов |
| MatPipes |
одномерный массив, содержащий 13 строковых констант - названий труб и ГОСТов |
| Diam |
двухмерный массив, содержащий 13 строк и 33 столбца. Номер строки соответствует определенному материалу труб, первый столбец (индекс 0) - содержит количество диаметров по сортаменту, все остальные элементы массива содержат величину внутреннего диаметра в миллиметрах (или 0) |
| PipeDiam |
двухмерный массив, по структуре и размерам совпадает с Diam, однако содержит строковые константы - условные диаметры труб |
49
Таблица 14.30
Формулы для расчета удельного сопротивления
| Трубы |
Формула |
| Стальные водогазопроводные и электросварные новые (коды материалов - 1 и 3) |
S0 =
| 0,001314 |
( |
1 + |
0,84 |
)0,226 |
| d5,226 |
ν |
|
| Чугунные напорные новые (код - 5) |
S0 =
| 0,00119 |
( |
1 + |
2,36 |
)0,284 |
| d5,284 |
ν |
|
| Стальные водогазопроводные и электросварные неновые, чугунные напорные неновые (коды- 2, 4, 6) |
S0 =
| 0,0014782 |
( |
1 + |
0,867 |
)0,3 |
| d5,3 |
ν |
(ν < 1,2 м/c)
S0 = (ν < 1,2 м/c) |
| Асбестоцементные (код - 7) |
S0 =
| 0,00091 |
( |
1 + |
3,51 |
)0,19 |
| d5,19 |
ν |
|
| Железобетонные виброгидропрессованные и со стальным сердечником (коды - 8, 9) |
S0 =
| 0,001301 |
( |
1 + |
3,51 |
)0,19 |
| d5,19 |
ν |
|
| Полиэтиленовые напорные (код - 10) |
S0 = |
| Стеклянные (код - 11) |
S0 = |
| Стальные и чугунные с цементно-песчаным покрытием (коды -12, 13) |
S0 =
| 0,001016 |
( |
1 + |
3,51 |
)0,19 |
| d5,19 |
ν |
|
Таблица 14.31
Коэффициенты для расчета предельных расходов
| Трубы |
п |
К |
Р |
alfa |
R |
b |
| Стальные |
1,9 |
0,001790 |
5,1 |
1,4 |
4,6 |
53 |
| Чугунные |
1,9 |
0,001790 |
5,1 |
1,6 |
3,3 |
107 |
| Асбестоцементные |
1,85 |
0,001180 |
4,89 |
1,95 |
7,3 |
78 |
| Железобетонные |
1,85 |
0,001688 |
4,89 |
1,30 |
3,3 |
100 |
| Пластмассовые |
1,774 |
0,001052 |
4,774 |
1,95 |
4,6 |
150 |
Таблица 14.32
Соответствие условных проходов и расчетных диаметров (мм)1
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Трубы стальные водогазопроводные ГОСТ 3262-75 |
| Dусл |
6 |
8 |
10 |
15 |
20 |
25 |
32 |
40 |
50 |
| Dpacч |
6,2 |
9,1 |
12,6 |
15,7 |
21,2 |
27,2 |
35,9 |
41,0 |
53,3 |
| (5,2) |
(8,1) |
(11,6) |
(14,7) |
(20,2) |
(26,1) |
(34,9) |
(40,0) |
(52,0) |
| Dусл |
65 |
80 |
90 |
100 |
125 |
150 |
|
|
|
| Dpacч |
67,5 |
80,5 |
93,3 |
105,0 |
131 |
156 |
|
|
|
| (66,5) |
(79,5) |
(92,3) |
(104,0) |
(130) |
(155) |
|
|
|
| Трубы стальные электросварные ГОСТ 10704-76 и ГОСТ 8696-74 |
| Dусл |
50 |
60 |
75 |
80 |
100 |
125 |
150 |
175 |
200 |
| Dpacч |
65 |
71 |
84 |
96 |
115 |
134 |
159 |
171 |
210 |
| (64) |
(70) |
(83) |
(95) |
(114) |
(133) |
(158) |
(170) |
(209) |
| Dусл |
250 |
300 |
350 |
400 |
450 |
500 |
600 |
700 |
800 |
50
Продолжение табл. 14.32
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Dpacч |
261 |
311 |
363 |
412 |
466 |
516 |
616 |
706 |
804 |
| (260) |
(311) |
(363) |
(412) |
(466) |
(516) |
(616) |
(706) |
(804) |
| Dyсл |
900 |
1000 |
1200 |
1400 |
1500 |
1600 |
|
|
|
| Dpacч |
904 |
1004 |
1202 |
1400 |
1500 |
1600 |
|
|
|
| (904) |
(1004) |
(1202) |
(1400) |
(1500) |
(1600) |
|
|
|
| Tрубы чугунные напорные ГОСТ 9583-75 |
| Dусл |
65 |
80 |
100 |
125 |
150 |
200 |
250 |
300 |
350 |
| Dрасч |
67,6 |
83,6 |
103,0 |
128,2 |
153,4 |
203,6 |
254,0 |
304,4 |
352,4 |
| (66,6) |
(82,6) |
(102,0) |
(127,2) |
(152,4) |
(202,3) |
(253,0) |
(304,4) |
(352,4) |
| Dусл |
400 |
450 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
| Dpacч |
401,4 |
450,6 |
500,8 |
600,2 |
699,4 |
799,8 |
899,2 |
998,4 |
|
| (401,4) |
(450,6) |
(500,8) |
(600,2) |
(699,4) |
(799,8) |
(899,2) |
(998,4) |
|
| Трубы асбестоцементные ГОСТ 539-80, класс ВТ9, тип 1 |
| Dусл |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
500 |
|
| Dрасч |
100 |
141 |
188 |
234 |
275 |
323 |
368 |
456 |
|
| Трубы железобетонные виброгидропрессованные ГОСТ 12586-83 |
| Dусл |
500 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
|
|
| Dpacч |
500 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
|
|
| Трубы железобетонные со стальным сердечником ГОСТ 26819-86 |
| Dусл |
250 |
300 |
400 |
500 |
600 |
|
|
|
|
| Dрасч |
230 |
293 |
394 |
461 |
590 |
|
|
|
|
| Трубы полиэтиленовые напорные ГОСТ 18599-83 |
| Dнаруж |
10 |
12 |
16 |
20 |
25 |
32 |
40 |
50 |
63 |
| Dpacч |
6,0 |
8,0 |
12,0 |
16,0 |
20,4 |
26,2 |
33,0 |
41,1 |
51,5 |
| DHaруж |
75 |
90 |
110 |
125 |
140 |
160 |
180 |
200 |
225 |
| Dрасч |
61,3 |
73,5 |
89,8 |
102,6 |
114,3 |
130,7 |
147,3 |
163,7 |
184,0 |
| Dнаруж |
250 |
280 |
315 |
355 |
400 |
450 |
500 |
560 |
630 |
| Dpacч |
204,5 |
229,0 |
280 |
315 |
355 |
400 |
462 |
517 |
582 |
| DHaруж |
710 |
800 |
900 |
1000 |
1200 |
|
|
|
|
| Dpacч |
656 |
738 |
830 |
921 |
1106 |
|
|
|
|
| Трубы стеклянные ГОСТ 8894-86 |
| Dусл |
40 |
50 |
80 |
100 |
150 |
200 |
|
|
|
| Dpacч |
36,0 |
56,0 |
79,5 |
106,0 |
148,0 |
195,5 |
|
|
|
| Трубы стальные с цементно-песчаным покрытием ГОСТ 10704-76 и 8696-74 |
| Dусл |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
600 |
700 |
| Dрасч |
198 |
249 |
297 |
349 |
396 |
450 |
500 |
598 |
688 |
| Dусл |
800 |
900 |
1000 |
1200 |
1400 |
1500 |
1600 |
|
|
| Dрасч |
784 |
882 |
980 |
1176 |
1374 |
1472 |
1572 |
|
|
| Трубы чугунные с цементно-песчаным покрытием ГОСТ 9583-75 |
| Dусл |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
600 |
700 |
| Dpacч |
204,6 |
255,0 |
292,9 |
340,9 |
389,9 |
439,1 |
489,3 |
588,7 |
687,9 |
| Dусл |
800 |
900 |
1000 |
|
|
|
|
|
|
| Dpacч |
786,3 |
863,2 |
982,4 |
|
|
|
|
|
|
Примечание. * - в скобках приведены расчетные диаметры для неновых труб
Ввод исходных данных
Перед вводом данных следует пронумеровать все узлы, участки и кольца на сети. Для проведения расчета требуются следующие исходные данные:
- - общее число участков в сети (CountAreas)
51
- - общее число узлов в сети (CountNodes);
- - общее число независимых колец (контуров), имеющихся в сети (CountRings);
- - наибольшее число участков в одном кольце (MaxCountAreas);
- - массив конфигурации сети Nodes: в первый столбец этого массива вводятся узлы начала каждого участка, во второй - узлы конца;
- - массив конфигурации колец Rings: в каждую строку массива (соответствующую одному кольцу) последовательно вводятся номера участков, составляющих это кольцо, причем номера участков, не совпадающие по направлению с движением воды в кольце по часовой стрелке, должны быть со знаком минус;
- - узловые расходы (массив Rashod), причем расход, направленный в узел (т.е., например, подача от НС), должен быть со знаком минус;
- - геодезические отметки узлов (массив Z);
- - длины участков (массив L);
- - коды материалов труб на участках (массив Mater);
- - коды диаметров труб на участках (массив NomerD);
- - необходимый свободный напор в узле (MinH);
- - минимальный диаметр при оптимизации (MinDiam);
- - шифр вида оптимизации (TypeOptini);
- - коэффициент суточной неравномерности водопотребления (Kday);
- - коэффициент часовой неравномерности водопотребления (Khour);
- - стоимость электроэнергии (Sigma);
- - срок окупаемости (Srok).
Начальное потокораспределение1
Метод, который часто применяется для компьютеризированного решения задачи начального потокораспределения, заключается в упрощении системы нелинейных уравнений баланса потерь напора в кольцах - замене их линейными и последующем решении системы /24/.
Линеаризованная модель описывается системой линейных алгебраических уравнений. Первые CountNodes уравнений системы строятся в соответствии с первым законом Кирхгофа для узлов, в соответствии с которым алгебраическая сумма расходов в каждом узле равна нулю:
Qi= Rashodj , j = 1, 2,..., CountNodes.(14.63)
Здесь Qi- расходы участков, связанных j-тым узлом.
Для решения системы из указанных уравнений можно использовать не все, а только CountNodes-1, поскольку одно из уравнений линейно зависит от остальных.
Другая группа уравнений, описывающих работу сети, базируется на втором законе Кирхгофа, в соответствии с которым сумма потерь напора на каждом из колец равна нулю:
SiQjβ = 0, j = 1, 2,..., CountRings, (14.64)
где Q - расходы участков, входящих в j-тое кольцо; Si - гидравлическое сопротивление i-того участка; β - показатель степени, равный 2.
Таких уравнений можно составить столько, сколько выделено колец, т.е. CountRings.
Решение систем нелинейных уравнений больших порядков сопряжено со значительными вычислительными трудностями, поэтому на начальном этапе расчета используют
52
линеаризованный вариант уравнении:
Si · Qi = 0, j = 1, 2,..., CountRings. (14.65)
Так как для вычисления величин удельных гидравлических сопротивлений нет данных о скоростях на участках, значения Si принимаются равными единице. Начальная цель расчета состоит в определении значений Qi для всех участков, т.е. для i = 1,2,..., CountAreas. Первые (CountNodes-1) уравнений строятся на использовании соотношения (14.63), а недостающие CountAreas-(CountNodes-1) уравнений - из соотношения (14.65).
Общий вид системы линейных алгебраических уравнений в матричной форме таков:
A · Q = B, (14.66)
Элементы свободных членов вектора В равны либо значениям расходов Rashodi (для первых CountNodes-1 уравнений), либо равны нулю для последних CountAreas-(CountNodes-1) уравнений. Элементы матрицы А формируются по массиву конфигурации Nodes и массиву колец Rings.
Для первых CountNodes-1 уравнений элементы матрицы А определяются по формулам:
Ai,j = -1, при i = Nodesj,1(14.67)
Ai,j= 1, при i = Nodesj,2(14.68)
Ai,j= 0, при Nodesj,1≠ Nodesj,2(14.69)
где i = 1, 2,...; CountNodes-1;j = 1, 2,..., CountAreas.
Первое условие соответствует участкам, по которым вода притекает к i-ому узлу, второе - участкам, по которым вода уходит от узла, третье - участкам, не связанным с узлом.
Для последних CountAreas-(CountNodes-1) уравнений элементы матрицы А равны:
Ai,j = 1, при j = Ringsk,j и Ringsk,j >0(14.70)
Ai,j = -1, при j = Ringsk,j и Ringsk,j<0(14.71)
Ai,j = 0, при j ≠ Ringsk,j(14.72)
Здесь:
k= 1, 2,..., CountRings (номер кольца);
i = CountNodes, CountNodes+1,..., CountAreas;
j = 1, 2,..., CountAreas.
Уравнение (14.70) выполняется тогда, когда направление обхода по k-ому кольцу и ток j-том участке совпадают, уравнение (14.71) - когда направления и ток противоположны, наконец, последнее уравнение соответствует участкам, которые не принадлежат k-тому кольцу.
По окончании формирования матрицы А выполняется решение системы линейных алгебраических уравнений (14.63 и 14.65). Такое решение всегда существует, поскольку матрица А хорошо обусловлена. Решение можно проводить любым из известных методов (Гаусса, Гивенса, Хаусхолдера).
Формирование матрицы и решение системы линейных уравнений производится с помощью двух подпрограмм - FillingA и BeginStreamAllocation.
Увязка сети методом Лобачева-Кросса
В результате решения системы (14.66) получаем вектор значений участковых расходов Q с точным балансом расходов в узлах, однако, поскольку в системе использовались
53
линеаризованные уравнения баланса потерь напора на кольцах, а в действительности эти уравнения нелинейны относительно расходов баланс потерь напора не соблюдается.
Для выполнения условия баланса потерь напора на кольцах производится перераспределение балансовых расходов - увязка расходов. Наиболее известным и простым методом увязки расходов по кольцам является метод Лобачева-Кросса /19/.
Увязка проводится в следующем порядке. Последовательно для каждого из контуров k = 1, 2,..., CountRings вычисляются невязки потерь напора на кольце (в идеальном случае сумма потерь напора на кольце должна равняться нулю, но в действительности это не так, поскольку расчет расходов проводился для линейной зависимости потери напора от участкового расхода):
Δhk =
Sj · Qj2(14.73)
Вычисляется поправка невязки k-того кольца:
ΔQk = - (14.74)
В формулах (14.73) и (14.74) L - элементы кольца, для которого выполняется увязка; Δhk соответствует массиву SigmaDH. Теперь вычисленные поправки включаются в соответствующие участковые расходы:
Qi = Qi - ΔQk при Ringsk,i>0.(14.75)
Qi = Qi + ΔQk при Ringsk,i<0.(14.76)
Процесс увязки имеет итерационный характер: каждый раз использование преобразований участковых расходов по формулам (14.73-14.76) уменьшает невязку потерь напора в каждом из колец. Итерационный процесс уменьшения невязок прерывается, как только будет выполнено условие:
max(Δhk) < ε,
где ε - абсолютная погрешность увязки (константа Epsilon).
Реализация алгоритма увязки сети реализована в виде подпрограммы Uvjazka, которая, в свою очередь, разбита еще на 5 подпрограмм:
CaseD - функция, возвращающая величину диаметра труб при заданном коде материала и номере диаметра в сортаменте;
CalcSO - функция, возвращающая удельное гидравлическое сопротивление труб при заданном коде материала и величине диаметра, а также скорости течения воды в трубе;
CalcDH - процедура, в которой вычисляются значения потерь напора на каждом участке;
ChangeConfig - процедура, в которой изменяется направление движения потоков на участках сети;
ChangeQ - процедура, в которой вычисляются поправочные расходы и происходит правка участковых расходов.
Блок-схема алгоритма подпрограммы Uvjazka приведена на рис. 14.16.
Оптимизация диаметров
Оптимизация диаметров водопроводных кольцевых сетей производится на основе технико-экономического расчета, предполагающего нахождение такого распределения диаметров и расходов, при котором приведенные затраты на строительство и эксплуатацию будут минимальными. Общее выражение для определения оптимального (наиболее экономически выгодного) диаметра на участке сети приведено в формуле 18.7.17.
54
На практике не совсем удобно рассчитывать диаметры по этой формуле, так как после вычисления их приходится округлять до ближайшего сортаментного диаметра. Более целесообразно пользоваться предельным расходом для данного диаметра - это наибольший расход, при котором выбранный диаметр оказывается экономически равноценен следующему сортаментному диаметру. Предельный расход можно рассчитывать по следующей формуле /14/:
Qпред =
| ( |
b |
) |
· |
( |
d2α - d1α |
) |
| β |
1/d1α - 1/d2α |
(14.77)
где b - коэффициент (табл. 14.31); d1 и d2 - меньший и больший смежные сортаментные диаметры; α и n - показатели степени, характеризующие режим работы труб; Р -коэффициент, определяемый по формуле /14/:
β =
24 · 365 ·103
|
σγK
|
| 102 |
η(1/T + R/100) |
(14.78)
здесь σ - стоимость электроэнергии (переменная Sigma); η - КПД насосных станций (константа Eta); R - сумма амортизационных отчислений (табл. 14.31); К - коэффициент (табл. 14.31); Т - срок окупаемости (переменная Srok); γ - коэффициент неравномерности расходования электроэнергии, определяемый по формуле (18.7.19).
Условия строительства и эксплуатации характеризует экономический фактор,
рассчитываемый по формуле:
Э = (14.79)
где p - показатель степени (табл. 14.31).
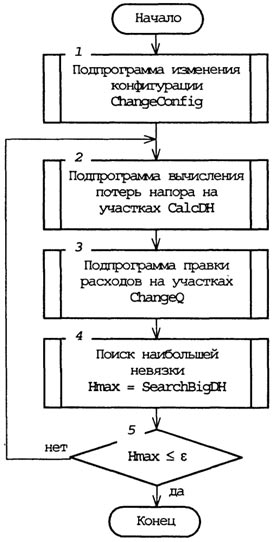
Рис. 14.16. Алгоритм увязки сети
Диаметр трубопровода на участке считается оптимальным, если его расход, во-первых, меньше предельного расхода для этого диаметра, во-вторых, больше предельного расхода для предыдущего по сортаменту диаметра.
Если расход больше, чем предельный для этого диаметра, происходит изменение диаметра на следующий по сортаменту. Если же расход, наоборот, меньше предельного расхода для предыдущего по сортаменту диаметра, происходит изменение диаметра на предыдущий. После этого производится увязка колец сети.
Таким образом, цикл "оптимизация-увязка" повторяется до тех пор, пока все диаметры труб после последней по времени оптимизации не останутся постоянными, и поэтому цель расчета - приведение в соответствие диаметров и предельных расходов -считается достигнутой.
Диаметры, с которых начинается оптимизация, могут задаваться тремя различными способами:
55
- - начальные диаметры на участках выбирает сам пользователь (переменная TypeOptim =1);
- - начальные диаметры на всех участках приравниваются к минимальным для данного вида труб (переменная TypeOptim = 2);
- - начальные диаметры на всех участках приравниваются к максимальным для данного вида труб (переменная TypeOptim = 3).
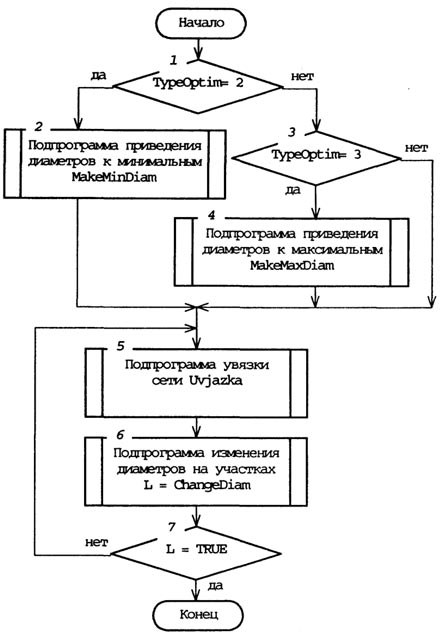
Рис. 14.17. Алгоритм оптимизации диаметров
Указанная последовательность действий легла в основу алгоритма подпрограммы Optimize, которая разбита еще на 3 подпрограммы:
ChangeDiam - функция, которая производит изменение диаметров на всех участках сети в соответствии с предельным расходом и возвращающая логическое значение
FALSE (ложь), если хотя бы на одном участке диаметр был изменен, или TRUE (правда), если такого изменения не было;
MakeMinDiam -процедура, приводящая диаметры на всех участках сети к минимальным;
MakeMaxDiam - процедура, приводящая диаметры на всех участках сети к максимальным.
Алгоритм подпрограммы Optimize приведен на рис. 14.17.
Определение свободных напоров в узлах*
Для определения свободного напора j-том узле, который связан с i-тым узлом участком, следует воспользоваться формулой:
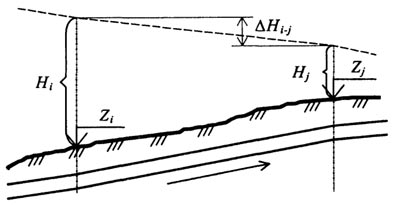
Рис. 14.18. Схема для расчета свободных напоров.
56
Hj = Hi + ΔHi-j + Zi - Zj(14.80)
где Hj и Hi - свободный напор в узлах; Zj и Zi - отметки поверхности земли в этих узлах; ΔHi-j - потери напора в трубопроводе на участке i-j.
Схема, иллюстрирующая формулу (14.80), приведена на рис. 14.18.
Для расчета свободных напоров во всех узлах сети предлагается следующий общий алгоритм: в узле номер 1 свободный напор первоначально принимается равным О, затем в соответствии с формулой (14.80) рассчитываются значения напоров во всех остальных узлах (без учета разности Zi - Zj). Следующий шаг - поиск наименьшего значения напора Т во всех узлах с учетом геодезических отметок, и, наконец, суммирование Т и необходимого напора MinH со свободными напорами узлов сети. Эта схема послужила основой алгоритма подпрограммы CalcH.
Общая часть программы WaterRings и дополнение к алгоритмам.
Алгоритм общей части программы WaterRings (рис. 14.19) начинается с ввода всех необходимых данных, затем следует обращение к подпрограммам формирования матрицы уравнений начального потокораспределения FillingA и решения этой системы BeginStreamAllocation (блоки 2, 3). В зависимости от выбранного пользователем метода оптимизации диаметров (блок 4) выполняется подпрограмма увязки участковых расходов Uvjazka или подпрограмма оптимизации Optimize (блоки 5, 6). Алгоритм заканчивается подпрограммой расчета свободных напоров CalcH и выводом на печать рассчитанных результатов.
Дополнение к алгоритмам
Как указано выше, при решении задачи
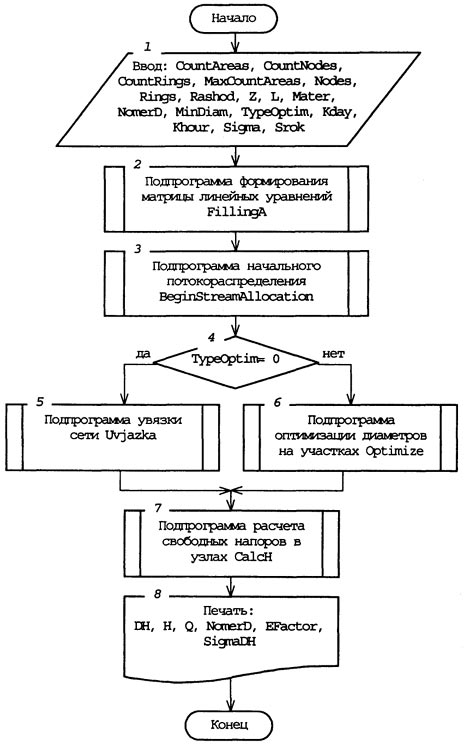
Рис. 14.19. Алгоритм расчета водопроводной кольцевой сети
57
начального потокораспределения была принята линеаризованная модель распределения расходов по участкам, причем значения удельных сопротивлений S трубопроводов приравнивались к единице из-за неопределенности скорости на участках. Если же рассчитать значение S при условной начальной скорости (например, 1 м/с), то линеаризованная модель еще больше приблизится к реальной и необходимое количество итераций при увязке сети уменьшится.
Примером создания компьютерной программы, реализующей указанные алгоритмы, служит программный комплекс PLUMBING, разработанный на кафедре водоснабжения и водоотведения Вологодского государственного технического университета. Пример расчета водопроводной кольцевой сети с двумя точками подачи воды и тупиком при помощи программы PLUMBING приведен в приложении 18.5.
58
1
- в скобках приведены расчетные диаметры для неновых труб.
1
В разделе использовались алгоритмы доцента (В.К. Королёнка)
