Первые работы по исследованию свойств ионообменных мембран и разработке теоретических основ многокамерного электродиализа опубликованы в первой половине нашего столетия [222, 223]. Отечественные разработки по электродиализу начаты в 1930-1935 гг. И.И. Жуковым. Попытки решения задач электромассопереноса через ионообменные мембраны вначале опирались на предположения о гомогенном строении материалов ионитов, допускающие постоянство кинетических параметров в толще мембраны и др. [98, 224, 225]. Однако в последние годы разработаны методы решения, учитывающие неоднородное строение ионитов [114, 226-228].
Наличие в ионообменных мембранах распределенных по объему фиксированных ионогенных групп приводит к зависимости от координат потенциальной энергии подвижных ионов. Минимальной энергией проти-воион обладает, находясь непосредственно у ионогенной группы; коион, напротив, в этом положении имеет максимальную потенциальную энергию. Поэтому перенос ионов по объему ионита сопряжен с преодолением ряда потенциальных барьеров. Под влиянием тепловых флуктуации отдельные противоионы могут приобрести достаточную энергию для отрыва от фиксированной группы и выхода из потенциальной ямы. При этом образуются свободная фиксированная группа (ионная вакансия) и "внедренный" ион. Таким образом, движение ионов в ионообменном материале по своему механизму напоминает движение ионов в кристалле. В то же время набухшие ионообменные мембраны содержат большое количество воды, что обеспечивает, по сравнению с кристаллами, аномально высокую степень диссоциации противоионов. Во многих мембранах отмечается также аномально высокая подвижность ионов водорода (в катионообменных) и гидроксила (в анионообменных).
Основываясь на представлениях о структуре ионита, сделано утверждение, что наиболее вероятными в ионообменных материалах являются три механизма переноса ионов: вакансионный, эстафетный и сольватационный [51, 274, 275]. В любом случае перенос ионов в мембране представляется, как совокупность скачков через некоторые потенциальные барьеры, что позволяет отождествлять элементарный акт переноса заряда и
75
массы в мембране с протеканием элементарного акта химической реакции и воспользоваться для описания переноса частиц теорией абсолютных скоростей реакции [276, 277].
Мы рассмотрим теорию массопереноса в электродиализной ячейке, исходя из стационарных условий процесса и однородного характера ионообменной мембраны [13]. На рис. 2.15 представлена электродиализная ячейка.
Средняя расчетная плотность тока по длине пути определяется выражением
(2.86)
где l - общая длина пути потока.
Связь площади мембраны FM, требуемой для достижения нужной степени деминерализации ΔС, пропускной способности установки Qуст и средней плотности тока iср определяется, согласно закона Фарадея, как
(2.87)
где F - число Фарадея;
η - выход по току, т.е. эффективность использования тока с целью "переброски" иона через мембрану.
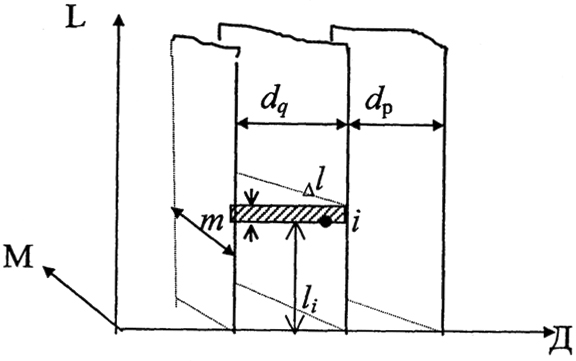
Рис. 2.15. Расчетная схема процесса деминерализации в электродиализной ячейке: LI - расстояние от входа в ячейку до i-ой точки; Δ1 - приращение длины: dq - толщина дилюатной камеры; dp - толщина рассольной камеры; т - ширина потока
76
Выход по току можно определить по отношению количества соли j, перешедшему с одной стороны мембраны на другую, к количеству прошедшего электричества, пропорциональному i,
(2.88)
Количественно поток ионов определяется из потоков в растворе и мембране. Например, для катионообменной мембраны он может быть рассчитан как
(2.89)
где Δj+ - убыль катионов на отдающей стороне мембраны.
Общую площадь мембран FM и пропускную способность установки представим в следующем виде:
FM=m·L·nM,
Qуст= V·m·da·nяч,
(2.90)
где пм - число мембран, V - скорость протекания дилюата, т - ширина потока, da - расстояние между мембранами, пяч - число ячеек. Подставив в выражение (2.87) уравнения (2.90), получим:
(2.91)
Плотность тока распределяется по длине ячейки в зависимости от содержания дилюата и рассола в соответствии с законом Ома. Значение средней плотности тока, учитывающее конструктивные параметры ячеек и прикладываемое напряжение
| iср= |
|
| 1 |
( |
| dq+ |
dq |
+(δa/χa+δк/χк)χNaCl |
| XN |
|
) |
| Cпр |
λ[1+0,02(T-290)] |
|
(2.92)
где uяч- падение напряжения;
XN - безразмерная величина, определяемая отношением концентраций рассола и дилюата в конце пути потока в аппарате, равна
β - коэффициент массопереноса;
Y- степень опреснения воды;
N- число ступеней опреснения;
77
Спр - концентрация раствора, соответствующая точке поляризации;
φ, χ - толщина и удельная электропроводность соответствующих мембран;
λ - эквивалентная электропроводность раствора;
T - температура.
Ранее указывалось, что при определенных условиях протекания электрохимического процесса, в т.ч. электродиализного, может возникнуть концентрационная поляризация (подразд. 2.6.1), появление которой связано с величиной плотности тока. Однако из экономических соображений целесообразно проводить электролиз при высоких плотностях тока (уменьшается площадь мембран (2.87), поэтому необходимо знать критические условия массопереноса в электродиализной ячейке, обусловленные появлением поляризации.
Возникновение концентрационной поляризации, т.е. критических условий, на границе раздела мембраны с раствором вследствие разности чисел переноса ионов в растворе и мембране определяют как
(2.93)
где D - коэффициент диффузии (иона, электролита); t -t- разность чисел переноса Z - валентного иона в мембране и растворе соответственно; δ, φ - критическая толщина диффузного слоя.
Формула (2.93) описывает условия, при которых концентрация раствора в непосредственной близости к мембране равна нулю. В правой части уравнения содержатся два параметра δкр и D, которые определяются гидродинамикой процесса и зависят от конструктивных и технологических условий. Для упрощения дальнейших расчетов примем, что коэффициент диффузии D в пределах диффузионного слоя постоянный и равен коэффициенту молекулярной диффузии.
Для определения максимальной толщины диффузного слоя (с учетом выражений (2.86), (2.87), (2.90)) предложена следующая формула [13].
| δкр = KL(D/v)1/3(Idq)0,25[v(l- |
h |
)]0,5·Vср-0,5, |
| dq |
(2.94)
и тогда критическая плотность тока
| iкр= |
ZFCпр·D |
| (t-t)K1(D/v)1/3(l·dq)0,25[v(1- )]0,5·Vср-0,5 |
(2.95)
78
где К1 - постоянная, определяемая конфигурацией перемычки;
Vср- средняя скорость протекания жидкости (дилюата);
v - кинематическая вязкость раствора;
l - расстояние между соседними перемычками-турбулизаторами;
h - высота сжатого сечения dq (см. рис. 2.16).
Рассмотрим единичный элемент лабиринтно-сетчатой прокладки, включающей участки "свободного" l и "сжатого" а сечения.
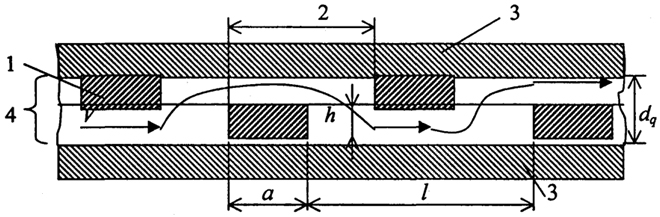
Рис. 2.16. Схема лабиринтно-сетчатой прокладки:
1 - перемычки-турбулизаторы;
2 - элемент;
3 - мембраны;
4 - прокладка
На участках элемента возникают четыре вида гидравлических сопротивлений, которые обусловливают общее гидравлическое сопротивление потоку в ячейке без учета распределенной системы.
Гидравлические сопротивления на участках между перемычками-турбулизаторами и в пределах самой перемычки влияют на общие потери напора на "свободном" и "сжатом" участках. Применив формулу Дарси-Вейсбаха для рассматриваемого примера, получим
| Hдл= |
A |
· |
l |
[ |
1- |
0,5 |
+ |
(1/Kэк -1) |
] |
· |
V2 |
| ReH |
4R |
Kэк |
(1 – h/dq)3 |
2g |
(2.96)
где А - коэффициент, зависящий от формы поперечного сечения;
ReH - число Рейнольдса, рассчитанное по гидравлическому радиусу канала R, ReH= 4VR/v;
Кэк - коэффициент экранирования, Кэк = 1/(1+(a/l)), зависит от типа прокладок.
Гидравлические сопротивления на участках с внезапным расширением и сжатием потока обусловливают потери напора на местные сопротивления в рассольных и дилюатных камерах
| Hм.с.=[ |
66,8 |
+ψ(( |
1/ξ-1 |
)2+( |
1 |
-1)2)]× |
V2 |
, |
| Re(h’)5 |
h’ |
h’·E |
2g |
(2.97)
79
где Re - число Рейнольдса, рассчитанное как
| Re= |
2Vdq |
, h’ = 1 - |
h |
, ψ= |
Re |
при Reкр = 7000 |
| v |
dq |
h’·Reкр |
Тогда общие потери напора в элементе прокладки складываются из
Нэл=Нмс+Ндл,
(2.98)
а потери напора по всей длине пути тока L в электродиализной ячейке равны
Н = пНэл,
(2.99)
где п - число элементов прокладки по всей длине пути потока L, п = 2L/(l+a) (здесь l - расстояние между перемычками на одной стороне мембраны,
а - длина перемычки (рис. 2.16).
80
