Рассмотрим кинетические закономерности, характерные для электрохимических процессов, обусловленных замедленным протеканием стадии переноса заряженных частиц, т.е. для электрохимического перенапряжения.
54
При равновесном потенциале анодный и катодный процессы протекают с одинаковыми скоростями, макроскопических (заметных) изменений в системе не происходит. Последние возможны только при потенциале, отличном от равновесного, когда скорости окисления и восстановления не равны друг другу. Разность этих скоростей и является общей скоростью процесса, которая тем больше, чем больше смещен потенциал от равновесного значения.
Найдем в общем виде зависимость между скоростью процесса и смещением потенциала электрода от равновесного значения.
Из учения о скоростях химических реакций известно, что скорость химической реакции на поверхности раздела твердой и жидкой фаз, отнесенная к единице поверхности, может быть выражена уравнением
V=k·e
·a’
(2.44)
где k - константа скорости;
а' - активность (или концентрация в случае достаточно разбавленного раствора) реагирующего вещества в слое жидкости, непосредственно прилегающем к поверхности твердого тела;
ω - энергия активации.
Уравнение (2.44) означает, что в реакцию вступают не все частицы вещества, находящиеся в сфере ее протекания, а только их часть, обладающая определенным запасом энергии, называемой энергией активации.
Удельную скорость электрохимической реакции выражают обычно через плотность тока: ia - скорость анодной реакции (окисления); iк - скорость катодной реакции (восстановления).
Плотность тока выражают в А/см2, А/дм2 или в А/м2, см2, дм2 и м2 -геометрическая площадь поверхности раздела электрод-раствор.
Предположим, что на границе электрод-раствор протекает реакция, в которой окислитель Ох принимает п электронов и превращается в восстановленную форму Red:
Ох + пе- ←→ Red
(2.45)
Уравнение (2.45) представляет собой обобщенную форму записи окислительно-восстановительной электрохимической реакции.
Для рассматриваемой реакции выражения для скоростей катодного и анодного процессов запишутся в виде:
ik=k1e
a’Ox,
(2.46)
ia=k2e
a’Red,
(2.47)
Это обычные уравнения химической кинетики, в которых входящая в них величина энергии активации зависит от потенциала электрода. В этом заключается важнейшая особенность электрохимических реакций, отличающая их от обычных химических реакций. Изменение потенциала
55
электрода, которое в известных пределах можно осуществлять по желанию, вызывает изменение энергии активации, т.е. изменяет скорость процесса.
Энергию активации электрохимических реакций можно представить состоящей из химического и электрического слагаемых:
ω = ω0 +ωэ.
(2.48)
Химическое слагаемое энергии активации ω0 соответствует равенству нулю скачка потенциала на границе раздела фаз электрод-раствор. Электрическое слагаемое ωэ появляется вследствие возникновения скачка потенциала на границе фаз. Однако на электрическую составляющую энергии активации влияет не весь скачок потенциала, а лишь та его часть, которая имеет место в плотной части двойного электрического слоя, т.е. (из (2.41)) ψ = φ-ψ1.
Это обусловлено тем, что в электрохимической реакции участвуют только частицы, находящиеся непосредственно у поверхности электрода в плотной части двойного электрического слоя.
Энергия электрического поля распределяется между двумя одновременно протекающими частными реакциями - катодной и анодной. Одна ее часть α действует на катодную реакцию, другая β - на анодную. Коэффициенты α и β называются коэффициентами переноса. Очевидно, что α + β=1.
Таким образом, электрическое слагаемое энергии активации для катодного процесса равно ωэ(к) = αzF(φ - ψ1), а для анодного - ωэ(а)= βzF(φ - ψ1).
Если возникший скачок потенциала отрицателен, то скорость катодной реакции возрастает, а анодной уменьшается. Учитывая это, энергию активации для катодной и анодной реакции можно представить в виде:
ωэ(к) = αzF(φ - ψ1)
(2.49)
ωэ(а)= βzF(φ - ψ1)
(2.50)
Кроме того, следует учесть, что активность (концентрация) ионов в плотной части двойного электрического слоя тоже зависит от его строения и связана с активностью ионов в объеме раствора а уравнением
a’ = ae
(2.51)
Обычно знак ψ1 потенциала противоположен знаку зарядов ионов в плотной части двойного электрического слоя. Следовательно, если ψ1 < 0 (катодная поляризация), то согласно уравнению (2.51) а’ох > aox, т.е. активность катионов в плотной части больше, чем в объеме.
Учитывая изложенное, выражения для скоростей катодного и анодного процессов (2.46) и (2.47) можно переписать в следующем виде:
ik=k1aoxe
e
e
(2.52)
56
ia=k2aRede
e
e
(2.53)
Уравнения (2.52) и (2.53) являются основными уравнениями электрохимической кинетики.
Так как для данной электрохимической реакции при определенных условиях величина химической составляющей энергии активации постоянна, то множитель e
в этих уравнениях можно ввести в константу и, объединив одинаковые сомножители, получим:
ik = k1’aOxe
e
(2.54)
ia = k2’aRede
e
(2.56)
Сдвиг потенциала от равновесного значения Δφ =φ - φр, следовательно, в уравнения (2.53) и (2.54) можно подставить φ = φр + Δφ.Тогда получим:
ik = k1’aOxe
e
e
(2.56)
ia = k2’aRede
e
e
(2.57)
Уравнения (2.52)-(2.57) могут описывать скорость любой электрохимической реакции.
При любом потенциале, отличном от равновесного, ia ≠ ik протекают два процесса, но с различными скоростями.
Например, если потенциал сдвинут в положительную сторону (анодная поляризация), то Δφ = φ - φр > 0 и, согласно уравнениям (2.56) и (2.57), iа > iк, т.е. скорость анодного процесса (окисления) больше скорости катодного процесса (восстановления). Суммарная скорость процесса окисления, выражаемая суммарной плотностью тока, равна
iA=ia-ik (2.58)
Если потенциал сдвинут в отрицательную сторону (катодная поляризация), то Δφ = φ - φр < 0 и, согласно уравнениям (2.56) и (2.57), ia < ik, т.е. скорость катодного процесса больше скорости анодного. Суммарная скорость процесса восстановления равна
iK=ik-ia (2.59)
Уравнения электрохимической кинетики удобно для наглядности представлять графически в виде поляризационных кривых. При допущении, что ψ1 = 0, уравнения (2.54) и (2.55) примут вид:
57
ik = k1’aOxe
(2.60)
ia = k2’aRede
(2.61)
На рис. 2.7 представлены частные поляризационные кривые, соответствующие зависимости скорости катодного и анодного процессов от потенциала электрода (2.60), (2.61), и суммарная поляризационная кривая, представляющая собой разность ia - ik для анодного и ik - ia для катодного процессов.
При φ = φр, ia = ik = 0.
При φ → -∞ (катодная поляризация) ia → 0, ik → ∞
При φ → ∞ (анодная поляризация) ia →∞, ik → 0.
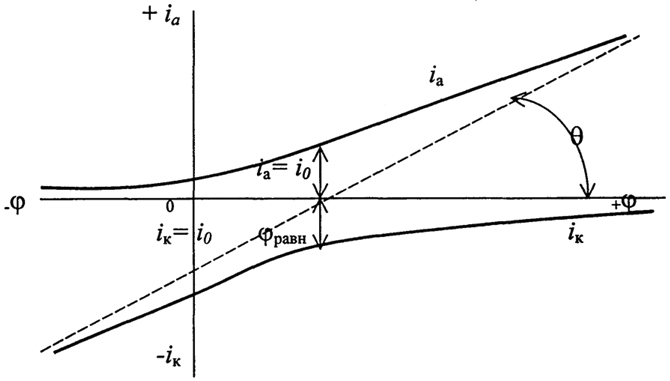
Рис. 2.7. Поляризационные кривые:
частные_____________; суммарные_ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Суммарная поляризационная кривая показывает, что электрохимический процесс может идти с определенной скоростью только при соответствующем сдвиге потенциала от равновесного значения. Амперметр, включенный в цепь, покажет отсутствие тока при φ = φр, а при других значениях потенциала будет показывать величину iA или iK.
Определенной скорости электрохимической реакции соответствует определенный сдвиг потенциала от равновесного значения, т.е. определенная величина перенапряжения.
Как видно из рис. 2.7, при значительных отклонениях потенциала электрода от равновесного значения суммарная поляризационная кривая
58
практически совпадает с частной поляризационной кривой. Это означает, что при достаточно большом сдвиге потенциала от равновесного значения в положительную сторону или при достаточно большой анодной поляризации iA ≈ ia (так как величина ik при этом пренебрежимо мала), соответственно при достаточно большой катодной поляризации iK ≈ ik (величина ia при этом пренебрежимо мала).
В этом случае уравнения электрохимической кинетики (2.56), (2.57) примут вид (при ψ1 = 0):
iK = ik = k10aOxe
,
(2.62)
iA = ia = k20aRede
,
(2.63)
где k10 = k1’e
; k
20 = k
2’e
.
Логарифмируя уравнения (2.62) и (2.63), получим:
для катодного процесса
-Δφ=
| - |
RT |
ln k10 |
- |
RT |
ln aox |
+ |
RT |
ln iK |
| αzF |
αzF |
αzF |
(2.64)
для анодного процесса
Δφ=
| - |
RT |
lnk20 |
- |
RT |
lnaRed |
+ |
RT |
lniA |
| βzF |
βzF |
βzF |
(2.62)
Объединив в уравнениях (2.64) и (2.65) постоянные величины для электродной реакции в данных условиях, т.е. lnk10;, lnk20;, lпа0х и lnaRed, перепишем их в следующем виде:
-Δφ = a + blniK,
(2.66)
где
| a = - |
RT |
lnk10 - |
RT |
lnaox; |
b= |
RT |
; |
| αzF |
αzF |
αzF |
Δφ = a + blniμ,
(2.67)
где
| a = - |
RT |
lnk10 - |
RT |
lnaox; |
b= |
RT |
| αzF |
αzF |
αzF |
Уравнения (2.66), (2.67) устанавливают связь перенапряжения с плотностью тока.
Уравнение вида (2.66) было впервые получено Тафелем при исследовании перенапряжения катодной реакции выделения водорода и носит его имя. Оно является обычным уравнением химической кинетики в логарифмической форме, отличающимся лишь тем, что энергия активации зависит от величины Δφ.
59
Согласно уравнениям (2.66), (2.67), в растворе с постоянной концентрацией величина перенапряжения данной электродной реакции должна линейно зависеть от логарифма плотности измеряемого тока. Причем угол наклона этой зависимости равен:
- для катодной реакции;
- для анодной реакции.
Постоянная a, входящая в уравнения (2.66) и (2.67), содержит логарифм константы скорости электрохимической реакции и, следовательно, в значительной степени определяется физической природой электрода.
Коэффициент b, как показывают опытные данные, практически не зависит от природы электрода и экспериментально найденное его значение в большинстве случаев совпадает с теоретическим при значениях коэффициентов переноса α и β, равных 1/2. Таким образом, определив экспериментально угол наклона зависимости Δφ - lni (т.е. коэффициент b), можно судить о числе электронов, принимающих участие в лимитирующей стадии реакции.
60
