Другое важное свойство электролитов - электропроводность. Различают удельную χ, Ом-1см-1 и эквивалентную λ, см2/Омг-экв электропроводности. На рис. 2.2 показана зависимость электропроводности с ростом концентрации для некоторых электролитов в водных растворах.
30
С ростом разбавления χ сначала увеличивается, так как увеличивается α. Когда α достигает большой величины, дальнейшее разбавление раствора будет вызывать уменьшение концентрации свободных ионов; удельная электропроводность начнет уменьшаться.
Зависимость между χ и λ выражается как
(2.7)
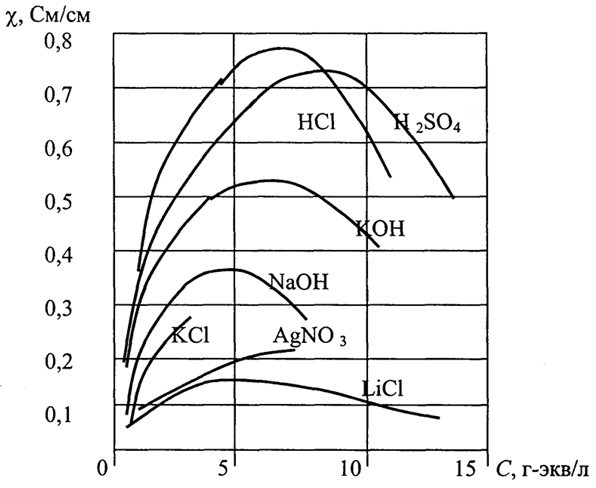
Рис.2.2. Зависимость удельной электропроводности некоторых растворов
от концентрации
Электропроводность электролитов зависит от температуры. Это влияние всегда приходится учитывать при практическом осуществлении электрохимических процессов. Зависимость эквивалентной электропроводности сильных электролитов от температуры определяется следующим уравнением
λt=α18[1 + k(t -18)],
(2.8)
где λ18 - электропроводность при 18 °С;
t - температура, при которой должна быть найдена λt;
k - температурный коэффициент.
31
При повышении температуры уменьшается вязкость среды, т.е. сопротивление ее движению ионов. Степень же диссоциации с ростом температуры несколько уменьшается вследствие понижения диэлектрической проницаемости растворителя, в частности, воды. Однако этот фактор оказывает меньшее влияние, чем уменьшение вязкости, почему и наблюдается рост электропроводности при нагревании.
Вышесказанное относится к слабым электролитам. Значительно сложнее дело обстоит с сильными электролитами (даже в разбавленных растворах). Степень диссоциации в таких растворах принимается равной 1, поэтому изменение электропроводности с концентрацией невозможно объяснить изменением числа ионов. В этом случае учитывают электростатическое взаимодействие между ионами. Для более простого случая одновалентного электролита эквивалентная электропроводность определяется по уравнению:
λ = λ∞-(А + Вλ)·√С,
(2.9)
где А и В- коэффициенты, зависящие от природы растворителя.
Прохождение электрического тока через раствор электролита вызывает направленное движение ионов к электродам. Катионы и анионы, имея противоположные знаки заряда и двигаясь навстречу друг другу, вызовут общий ток
i = ik+ia = αCF(vk + va)
(2.10)
где vk и va - скорости движения катионов и анионов, см/с.
Если скорость движения ионов заменить на их подвижность и =F·v*, а напряженность электрического поля будет равна 1 В/см, то
i = χ = αС(uk+ua)
(2.11)
или через эквивалентную электропроводность
λ = α(uk+ua)
(2.12)
При бесконечном разведении, когда α = 1,
λ∞=uk0 + ua0 = λk + λa,
(2.13)
где λ∞, λk, λa, - электропроводности раствора и ионов при бесконечном разведении;
uk0 + ua0 - предельные подвижности ионов.
32
Уравнения (2.12) и (2.13) отражают закон Кольрауша, физическая сущность которого состоит в том, что в растворе электролита катионы и анионы переносят электрический ток независимо друг от друга. Ниже приведены предельные эквивалентные электропроводности водных растворов электролитов, т.е. бесконечно разбавленных, при 25 °С.
Таблица 2.1
Предельные эквивалентные электропроводности водных растворов
электролитов
| Электролит |
λ∞ |
Электролит |
λ∞ |
Электролит |
λ∞ |
| H2SO4 |
429,8 |
КОН |
271,1 |
НСl |
149,0 |
| НС1 |
426,2 |
NH4OH |
271,0 |
КМО3 |
145,0 |
| HNO3 |
421,2 |
NaOH |
247,8 |
NaOH |
126,4 |
Как следует из закона Кольрауша, эквивалентная электропроводность определяется суммой электропроводностей катиона и аниона (2.13).
Для нахождения электропроводности отдельного иона необходимо знать долю тока, переносимую этим ионом, или так называемое число переноса иона ti.. Для бинарного электролита (например, NaCl) числа переносов для катиона и аниона определяются соответственно как
| tk= |
ik |
= |
uk |
= |
αk |
| i |
uk + ua |
λk + λa |
| ta= |
ia |
= |
ua |
= |
αa,k |
; tk + ta =1 |
| i |
uk + ua |
λk + λa |
(2.14)
Числа переноса ионов определяют несколькими методами. Наиболее известные из них - это метод Гитторфа, метод движущейся границы и метод ЭДС [36, 37].
Сравнив выражения (2.13) и (2.14), можно получить зависимость чисел переноса от эквивалентной электрической проводимости при любой концентрации бинарного электролита:
| tk0= |
λk0 |
и |
ta0= |
λa0 |
| λ∞ |
λ∞ |
(2.15)
где tk0, ta0 -предельные числа переноса.
Числа переноса, определенные по методу Гитторфа, фактически
33
являются эффективными (или кажущимися) числами переноса. Для определения истинных чисел переноса необходимо учитывать сольватационный перенос растворителя при движении ионов, что отражается на изменении концентрации в приэлектродных и примембранных областях [37]. Различие между эффективными и истинными числами переноса велико в высококонцентрированных растворах и уменьшается с разбавлением. В пределе, при бесконечном разведении, они должны совпадать. В дальнейшем мы будем говорить об эффективных числах переноса.
Из экспериментальных данных следует, что числа переноса зависят от концентрации электролита, хотя и в меньшей степени, чем от электропроводности. Если t°i= 0,5, то при увеличении концентрации раствора число переноса практически не изменяется. Если t°i<0,5, то с ростом концентрации соли эффективное число переноса уменьшается, а при t°i> 0,5 - увеличивается. Повышение температуры также влияет на числа переноса. В поведении ионов при бесконечном разбавлении обнаруживаются следующие закономерности: 1) увеличение подвижности ионов при повышении температуры; 2) наличие максимума на кривой зависимости предельной электропроводности (или подвижности) от кристаллографического радиуса (табл. 2.2).
Таблица 2.2
Предельная электропроводность ионов в водных растворах при 25°С
| Ион |
H+ |
½Zn2+ |
½Cd2+ |
Li+ |
Na+ |
K+ |
Rb+ |
Cs+ |
½Cu2+ |
Ag+ |
ri, E
λi°, См·с
м2/г-экв |
0,00
349,8 |
0,83
53,5 |
0,99
54 |
0,68
38,7 |
0,98
50,1 |
1,33
73,5 |
1,49
77,5 |
1,65
76,8 |
0,8
54 |
1,13
61,9 |
| Ион |
½Mg2+ |
½Ca2+ |
½Al3+ |
½Pb2+ |
½Fe2+ |
1/3Fe3+ |
½Ni2+ |
NH4+ |
[(C2H5)4N]+ |
[(CH3)4N]+ |
ri, E
λi° |
53,06 |
59,9 |
0,57
63 |
1,26
70 |
0,80
53,5 |
0,67
68 |
0,74
54 |
-
73,7 |
-
32,7 |
-
44,9 |
| Ион |
F- |
Cl- |
Br- |
I- |
OH- |
ClO4- |
NO3- |
H2PO4- |
CH3COO- |
½SO4- |
½HPO4- |
ri, E
λi° |
1,23
55,4 |
1,81
76,3 |
1,96
78,3 |
2,20
76,8 |
-
197,6 |
-
68 |
-
71,4 |
-
36 |
-
40,9 |
-80 |
-
57,0 |
34
Из табл. 2.2 следует, что в ряду ионов одинаковой валентности подвижность в основном возрастает с увеличением ионного радиуса. Обусловлено это тем, что радиусы ионов в растворе вследствие гидратации отличаются от кристаллографических. Чем меньше ион, тем больше он гидратирован (радиус гидратированного Li+ меньше радиуса гидратированного Na+ и т.д.). Однако, если собственный размер иона возрастает настолько, что прочная гидратная оболочка вокруг него уже не удерживается, то при дальнейшем увеличении кристаллографического радиуса подвижность ионов уменьшается. Это наблюдается для однозарядных катионов от Cs+ к [(CH3)4N]+ и для анионов от Br- к I- и далее Н2РО4-. Ионы водорода и гидроксила обладают аномально высокими подвижностями, превышающими остальные в 3-8 раз [38, 135].
35
*
Подвижность иона электрическая, u
i, см
2сек
-1В
-1, определяет среднюю скорость движения иона
vi, см·сек
-1, при единичной напряженности электрического поля, равной 1 В/см.
